Diện tích hình tròn: công thức, ví dụ, bài tập hay

Diện tích hình tròn là kiến thức hình học nền tảng mà học sinh nào cũng cần nắm vững để làm tốt bài tập từ cơ bản đến nâng cao. Khi hiểu đúng bản chất, bạn không chỉ nhớ được công thức mà còn biết vận dụng linh hoạt vào nhiều tình huống thực tế. Bài viết này sẽ giúp bạn hệ thống lại lý thuyết, ví dụ minh họa và mẹo học hiệu quả.

Diện tích hình tròn là gì?

Khái niệm và ký hiệu cơ bản

Trong hình học phẳng, Diện tích hình tròn được hiểu là phần bề mặt nằm bên trong đường tròn có bán kính cho trước. Thông thường, diện tích được ký hiệu là S, còn bán kính ký hiệu là r. Khi nói đến một đường tròn bất kỳ, ta luôn quan tâm đến cặp giá trị S và r để mô tả kích thước của nó.

Bán kính, đường kính và số pi

Để tính diện tích của một đường tròn, bạn cần hiểu mối liên hệ giữa bán kính, đường kính và số pi. Bán kính là khoảng cách từ tâm đến mọi điểm trên đường tròn, còn đường kính gấp đôi bán kính nên được ký hiệu là d = 2r. Số pi, thường lấy xấp xỉ 3,14 hoặc dùng ký hiệu π, đóng vai trò là hằng số quan trọng xuất hiện trong mọi công thức liên quan đến đường tròn.

Diện tích hình tròn công thức và cách suy ra

Công thức chuẩn trong chương trình phổ thông

Công thức quen thuộc nhất để tính Diện tích hình tròn là S = π.r², trong đó r là bán kính của đường tròn. Khi áp dụng vào bài tập, bạn chỉ cần xác định đúng bán kính, thay số pi theo yêu cầu đề bài và tính toán cẩn thận. Nếu đề bài cho đường kính, bạn nhớ đổi sang bán kính bằng cách lấy r = d/2 rồi mới thay vào công thức.

Giải thích trực quan dễ hiểu

Nhiều giáo viên thường dùng cách cắt ghép hình tròn thành các hình gần giống hình chữ nhật để giải thích vì sao diện tích lại bằng π.r². Khi chia đường tròn thành nhiều “miếng quạt” nhỏ và xếp xen kẽ, ta thu được một hình gần như hình chữ nhật có chiều dài xấp xỉ nửa chu vi, còn chiều rộng gần bằng bán kính. Từ đó, diện tích hình mới gần bằng chu vi nhân bán kính chia hai, tức là π.d.r/2 và sau khi rút gọn sẽ trở thành π.r².

Cách tính diện tích hình tròn qua ví dụ

Ví dụ cơ bản từng bước

Giả sử bạn cần tính Diện tích hình tròn có bán kính r = 5 cm trong một bài kiểm tra. Trước hết, bạn ghi lại công thức S = π.r² để tránh nhầm lẫn trong quá trình trình bày. Sau đó, bạn thay r = 5 vào, ta được S = π.5² = 25π, và nếu lấy π ≈ 3,14 thì S ≈ 78,5 cm², nhớ ghi kèm đơn vị diện tích đầy đủ.

Bài toán có dữ kiện là đường kính

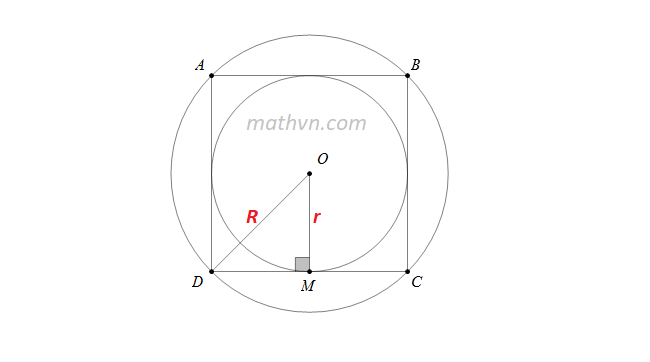
Nếu đề bài cho đường kính d = 10 cm thay vì bán kính, bạn cần thêm một bước trung gian nhỏ. Đầu tiên, tính bán kính bằng cách lấy r = d/2 = 5 cm rồi áp dụng công thức quen thuộc để tìm diện tích của đường tròn. Cách làm này giúp bạn rèn thói quen xử lý dữ kiện linh hoạt, tránh tình trạng nhầm lẫn giữa r và d trong quá trình giải toán.

Bài toán ngược và bài tập tổng hợp

Ở mức độ nâng cao hơn, đề bài có thể cho diện tích trước và yêu cầu tìm bán kính hoặc đường kính tương ứng. Khi đó, bạn chỉ cần biến đổi công thức Diện tích hình tròn thành r = √(S/π) rồi thay số vào để tính toán. Ngoài ra, nhiều đề tổng hợp còn kết hợp thêm chu vi đường tròn, hình quạt tròn hoặc so sánh diện tích các hình khác nhau để kiểm tra khả năng tư duy của học sinh.

Ứng dụng diện tích hình tròn trong đời sống

Từ lớp học đến thực tế xung quanh

Kiến thức về Diện tích hình tròn không chỉ xuất hiện trong sách giáo khoa mà còn liên quan trực tiếp đến nhiều đồ vật quen thuộc. Khi muốn tính diện tích mặt bàn tròn, nắp cống, miệng giếng hay đĩa tròn, bạn đều phải đo bán kính rồi áp dụng đúng công thức. Nhờ đó, chúng ta có thể ước lượng được lượng sơn cần dùng, diện tích phủ của vật liệu hay không gian chiếm chỗ trong thực tế.

Một số lưu ý khi làm bài kiểm tra

Khi giải các bài toán liên quan đến Diện tích hình tròn, học sinh thường hay mắc lỗi quên bình phương bán kính hoặc nhầm giữa bán kính và đường kính. Một sai lầm khác là quên ghi đơn vị diện tích, chẳng hạn như cm² hoặc m², khiến bài làm bị trừ điểm đáng tiếc. Vì vậy, bạn nên trình bày lần lượt theo các bước: ghi công thức tổng quát, thay số đúng, tính toán rõ ràng và kiểm tra lại kết quả trước khi nộp bài tại khiphach.

Mẹo ghi nhớ công thức nhanh

Để không quên Diện tích hình tròn, bạn có thể gắn công thức với một câu “thần chú” ngắn như “pi nhân r bình là xong”. Khi làm bài, hãy luôn viết lại công thức S = π.r² trước rồi mới thay số vào để tạo phản xạ tự nhiên. Thường xuyên luyện tập với nhiều dạng bài khác nhau cũng giúp bạn khắc sâu kiến thức lâu dài hơn.